Given the functions

To decide whether or not the functions are inverses of each other,
Solving f(x) inversely i.e to give f⁻¹(x)
Where f(x) = y
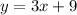
Replace y with x and x with y to give
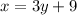
Solve for y i.e make y the subject
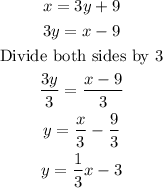
The inverse of f(x) i.e f⁻¹(x) is
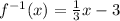
From the above deductions, it can be seen that g(x) is the inverse of f(x), i.e g(x) = f⁻¹(x)
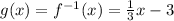
Thus, the functions are inverse of each other.
The answer is Yes.