a) Consider the experiment of picking 3 tax returns at random as 3 related experiments (due to the fact that it is without replacement); then, as for the first time one selects a tax return,
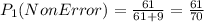
As for the second time we grab a tax return, there are 69 tax returns in total and 9 of them contain errors; thus,
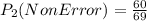
Similarly, as for the third picking round,
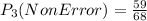
Finally, the probability of experiment a) is
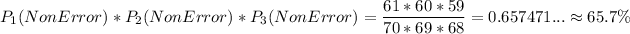
Rounded to one decimal place, the probability of event a) is 65.7%
b) Similarly, in the event of all three tax returns containing errors,

Thus,
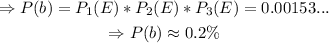
The probability of event b) is 0.2%. It is quite unusual.
c) The condition 'at least one of those containing errors' includes the cases when 1, 2, or 3 tax returns of the ones selected have errors. Notice that
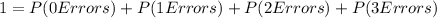
Therefore,
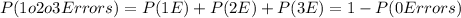
And we found the probability of picking 3 tax returns without any errors in part a); thus,

The probability of event c) is 34.3%.
d) Analogously to part c), the probability of selecting at least one without errors is
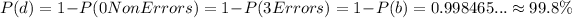
The probability of event d) is 99.8%, and it is not improbable at all.