Since the acceleration of the of the bosled is constant the entire motion this is an uniformaly accelerated motion which means that we can use the following equations:
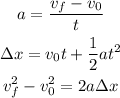
We want to know how long it takes for the bobsled to reach the midway to determine this we first need to determine the acceleration of the bobsled. We know that the incline is 25.1 m long which means that we know the change in position, we also know that it started from rest and hence the initial velocity is zero; also, we know that it takes 8.68 s to move all this way then we know the time for the entire motion. This means that we can use the second equation to determine the acceleration:

Hence, the acceleration of the bobsled is 0.67 m/s².
Now that we know the acceleration of the bobsled along the incline we can use the second equation to determine how long it takes to reach the midway which would be when it travels 12.55 m, then we have:

Therefore, it takes 6.14 s to reach the midway