ANSWER
The half-life of the sample is 50 days
Step-by-step explanation
Given thanks
The initial mass of the sample is 100g
The remaining mass of the sample is 25g
Time = 4 days
To find the half-life of the mass, follow the steps below
Step 1: Write the half life formula
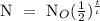
Where

Step 2: Substitute the given data to find the half-life of the sample
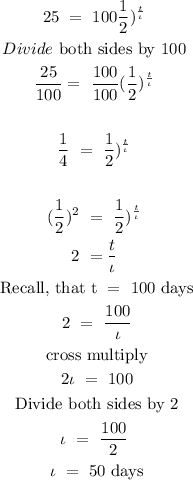
Hence, the half-life of the sample is 50 days