Question

if a 100g sample of a radioactive element decays to 25g in 4 days what is the half life of the element?

Answer 1

The half-life of the sample is 50 days

Step-by-step explanation

Given thanks

The initial mass of the sample is 100g

The remaining mass of the sample is 25g

Time = 4 days

To find the half-life of the mass, follow the steps below

Step 1: Write the half life formula

`\text{ N }=\text{ N}_O((1)/(2))^{(t)/(\iota)}`

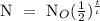
Where

`\begin{gathered} \text{ N is the undecayed sample} \\ \text{ N}_O\text{ is the decayed sample} \\ \iota\text{ is the half-life} \end{gathered}`

Step 2: Substitute the given data to find the half-life of the sample

`\begin{gathered} 25\text{ }=\text{ 100\lparen}(1)/(2))^{(t)/(\iota)} \\ Divide\text{ both sides by 100} \\ (25)/(100)=\text{ }(100)/(100)((1)/(2))^{(t)/(\iota)} \\ \\ (1)/(4)\text{ }=\text{ \lparen}(1)/(2))^{(t)/(\iota)} \\ \\ ((1)/(2))^2\text{ }=\text{ \lparen}(1)/(2))^{(t)/(\iota)} \\ 2\text{ }=(t)/(\iota) \\ \text{ Recall, that t }=\text{ 100 days} \\ \text{ 2 }=\text{ }(100)/(\iota) \\ \text{ cross multiply} \\ \text{ 2}\iota\text{ }=\text{ 100} \\ \text{ Divide both sides by 2} \\ \iota\text{ }=\text{ }(100)/(2) \\ \text{ }\iota\text{ }=\text{ 50 days} \end{gathered}`

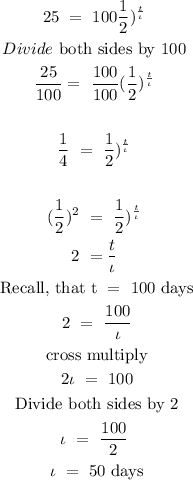
Hence, the half-life of the sample is 50 days