The common complex number to both lines is
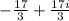 .
.
Let's calculate the complex numbers corresponding to the endpoints of each line segment.
For the first line segment:
Endpoint 1: (-3, 3)
Endpoint 2: (4, -4)
The complex number corresponding to a point (a, b) in the complex plane is a + bi. Therefore:
Endpoint 1 corresponds to the complex number -3 + 3i.
Endpoint 2 corresponds to the complex number 4 - 4i.
For the second line segment:
Endpoint 1: (5, 7)
Endpoint 2: (-2, -7)
The complex number corresponding to each point:
Endpoint 1 corresponds to the complex number 5 + 7i.
Endpoint 2 corresponds to the complex number -2 - 7i.
Now, let's find the complex number that is common to both lines, i.e., the intersection point of these lines. To find the intersection, we need to find where the equations representing these lines intersect, assuming they continue infinitely in both directions.
The equation of the line passing through two points
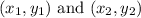 is given by:
is given by:
![\[y - y_1 = \frac{{y_2 - y_1}}{{x_2 - x_1}} (x - x_1)\]](https://img.qammunity.org/2023/formulas/mathematics/college/kkoygrp445a98km6zo5ph4kewoq3cjnmcf.png)
Let's find the intersection point of the lines formed by these complex numbers:
For the first line:
![\[\frac{{-4 - 3}}{{4 - (-3)}} = \frac{{-7}}{{7}} = -1\]](https://img.qammunity.org/2023/formulas/mathematics/college/y59px7skku2cbfesdzvhdsefs7x1tknbem.png)
So, the equation for the first line segment is y = -x.
For the second line:
![\[\frac{{-7 - 7}}{{-2 - 5}} = \frac{{-14}}{{-7}} = 2\]](https://img.qammunity.org/2023/formulas/mathematics/college/t56znh5f5yg7j4mb90wfyer5h264koxnvd.png)
So, the equation for the second line segment is y = 2x + 17.
To find the common complex number (intersection point), we need to solve these equations simultaneously:
y = -x
y = 2x + 17
Solving these equations, we find x = -17/3 and y = 17/3.
Therefore, the common complex number to both lines is -17/3 + 17i/3.