Question

`f(x) = {x}^(3) - 3x { }^(2)`find the zeros. and show all work please

Answer 1

Given the function:

`f(x)=x^3-3x^2`

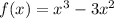
The zeros of the function can be said to be the x-intercept of the given function.

To find the zeros, substitute 0 for f(x) and evaluate.

We have:

`\begin{gathered} 0=x^3-3x^2 \\ \\ \text{ Factor out x}^2 \\ \\ x^2(x-3)=0 \end{gathered}`

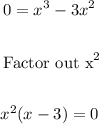
We have the individual factors:

`\begin{gathered} x^2 \\ (x-3) \end{gathered}`

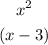
Equate the individual factors to zero:

`\begin{gathered} x^2=0 \\ x-3=0 \end{gathered}`

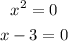
Solve each factor for x:

`\begin{gathered} x^2=0 \\ \text{Take the square root of both sides:} \\ \sqrt[]{x^2}=\sqrt[]{0} \\ x=0 \\ \\ \\ x-3=0 \\ \text{Add 3 to both sides:} \\ x-3+3=0+3 \\ x=3 \end{gathered}`

Therefore, the zeros of the function are:

x = 0, 3

In point form, the zeros are:

(0, 0) and (3, 0)

ANSWER:

x = 0, 3