Question

There are 98 national monuments in particular country eighty six of these monuments are located in state A

Answer 1

From our exercise we know that

• In a country we have a total of 98 monuments

,

• In a state of this country there are 86 monuments

a) What a fraction of the national monuments can be found in state A

`(86)/(98)=0.877`

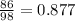
In state A are 87.7% of the country's monuments

a) The answer is 0.877

b) How many of the national monuments in the country are found outside state A

`\begin{gathered} OutsideA=Total-stateA \\ OutsideA=98-87 \\ OutsideA=12 \end{gathered}`

There are 12 monuments that are outside of state A

b) the answer is 12

c) Write the fraction of national monuments found in states other than state A

`(12)/(98)=0.122`

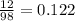
Outside state A are 12.2% of the country's museums

c) the answer is 0.122