From our exercise we know that
• In a country we have a total of 98 monuments
,
• In a state of this country there are 86 monuments
a) What a fraction of the national monuments can be found in state A
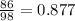
In state A are 87.7% of the country's monuments
a) The answer is 0.877
b) How many of the national monuments in the country are found outside state A
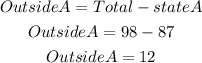
There are 12 monuments that are outside of state A
b) the answer is 12
c) Write the fraction of national monuments found in states other than state A
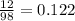
Outside state A are 12.2% of the country's museums
c) the answer is 0.122