Question

A formula for the stopping distancean average car iss=(x^2/20) + xwhere s is the stopping distance in feet and x is the car's speed in miles per hour.If a car is 75 feet from an intersection at which it must stop, what is the maximum speed it can be traveling? A. 60 miles per hourB. 50 miles per hourC. 40 miles per hour D. 30 miles per hour E.20 miles per hour

Answer 1

Given:

`s=(x^2)/(20)+x`

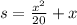
Where:

s is the stopping distance

x is the speed of the car

If the car is 75 feet from an intersection at wich it must stop, let's find the maximum speed.

Here, the stopping distance, s = 75 feet

To find the maximum speed, x, substitute 75 for s and solve for x.

We have:

`\begin{gathered} s=(x^2)/(20)+x \\ \\ 75=(x^2)/(20)+x \end{gathered}`

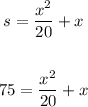
Multiply all terms by 20:

`\begin{gathered} 75\ast20=(x^2)/(20)\ast20+x\ast20 \\ \\ 1500=x^2+20x \end{gathered}`

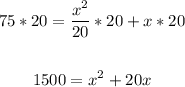
Rewrite the equation:

`x^2+20x=1500`

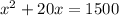
Subtract 1500 from both sides to equate to zero:

`\begin{gathered} x^2+20x-1500=1500-1500 \\ \\ x^2+20x-1500=0 \end{gathered}`

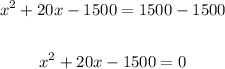
Factorize the right hand side of the equation:

`(x-30)(x+50)=0`

Take the individual factors:

(x - 30) = 0

(x + 50) = 0

x - 30 = 0

Add 30 to both sides:

x - 30 + 30 = 0 + 30

x = 30

x + 50 = 0

Subtract 50 from both sides:

x + 50 - 50 = 0 - 50

x = -50

We have:

x = 30,

x = -50

Since the speed cannot be a negative value, let's take the positive value.

Therefore, the speed is 30 miles per hour

ANSWER:

D. 30 miles per hour