Given:
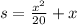
Where:
s is the stopping distance
x is the speed of the car
If the car is 75 feet from an intersection at wich it must stop, let's find the maximum speed.
Here, the stopping distance, s = 75 feet
To find the maximum speed, x, substitute 75 for s and solve for x.
We have:
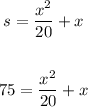
Multiply all terms by 20:
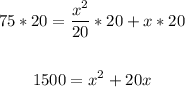
Rewrite the equation:
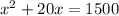
Subtract 1500 from both sides to equate to zero:
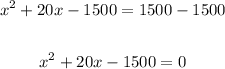
Factorize the right hand side of the equation:
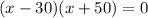
Take the individual factors:
(x - 30) = 0
(x + 50) = 0
x - 30 = 0
Add 30 to both sides:
x - 30 + 30 = 0 + 30
x = 30
x + 50 = 0
Subtract 50 from both sides:
x + 50 - 50 = 0 - 50
x = -50
We have:
x = 30,
x = -50
Since the speed cannot be a negative value, let's take the positive value.
Therefore, the speed is 30 miles per hour
ANSWER:
D. 30 miles per hour