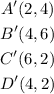Given the Pre-Image ABCD, you can identify that the coordinates of its vertices are:
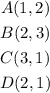
You need to dilate it using this scale factor (the Dilation must be centered at the Origin):
By definition, a Dilation is a transformation in which the Image and the Pre-Image have different sizes, but they have the same shape.
In order to dilate ABCD, you need to multiply each coordinate of its vertices by the scale factor. By doing this, you will find the coordinates of the vertices of the Image A'B'C'D':
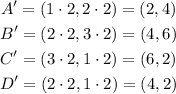
Hence, the answer is: