From the given information, the sketch of the problem is shown below:
It is required to find the distance between points A and B.
The sum of angles in a triangle is 180º, it follows that:
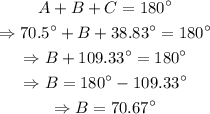
Recall from the Law of Sines that the following equation holds:

Substitute the angle measures and side length into the equation:
