Question

(1 point)(You will need a calculator.) Suppose you deposit $134,000 into an account paying 7.7% simple annual interest, and that you won'ttouch the account until it-holds $1,000,000. How long must you wait?Answer:years. (Round your answer to the nearest year.)

Answer 1

The simple interest formula is as follows:

`I=P\cdot r\cdot t`

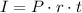
Where P is the principal amount (the initial amount), r is the annual rate and t is the time in years.

The final amount is the initial amount plus the interest, so:

`\begin{gathered} V=P+I \\ V=P+P\cdot r\cdot t \\ V=P(1+rt) \end{gathered}`

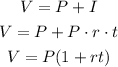
We have the princiapl value $134,000, the final value $1,000,000 and the rate of 7.7%, so:

`\begin{gathered} V=1000000 \\ P=134000 \\ r=7.7\%=0.077 \end{gathered}`

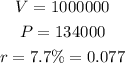
So, we can solve for t and input the values:

`\begin{gathered} V=P(1+rt) \\ \frac{V}{P_{}}=1+rt \\ rt=(V)/(P)-1 \\ t=((V)/(P)-1)/(r) \end{gathered}`
`\begin{gathered} t=((1000000)/(134000)-1)/(0.077) \\ t=(7.4626\ldots-1)/(0.077) \\ t=(6.4626\ldots)/(0.077) \\ t=83.93\ldots\approx84 \end{gathered}`

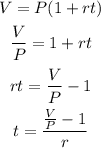
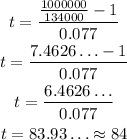
So, you must wait approximately 84 years.