Question

4. What value of c would make the function below have two real solutions? y= -3x^2 – 4x+c

Answer 1

The quadratic equation is,

`y=-3x^2-4x+c`

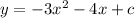
The value of coefficients of square term, x term and constant terms are,

a = -3

b = -4

and c = c.

For two real roots,

`b^2-4ac>0`

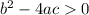
Dubstitute the values in the equation to obtain the value of c.

`\begin{gathered} (-4)^2-4\cdot(-3)\cdot(c)>0 \\ 16+12c-16>0-16 \\ (12c)/(12)>(-16)/(12) \\ c>-1.333 \end{gathered}`

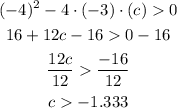
So value of c should be greater than -1.333, and from from the options it can be observed that value more than -1.333 is only c = -1.

So answer is c = -1.