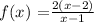Question

Write an equation for a rational function whose graph has all of the indicated features.vertical asymptote with equation x =1, horizontal asymptote with equation y =2, x-intercept of 2 and y-intercept of 4

Answer 1

Given:

The rational function has the following features:

1. A vertical asymptote with equation x =1

2. A horizontal asymptote with equation y =2

3. x-intercept of 2 and y-intercept of 4

Let's begin with the numerator of the rational function:

The x-intercept is the point where the graph cuts the x-axis

Given that the x-intercept is 2, the numerator has a factor of (x-2)

`\begin{gathered} x\text{ =2} \\ x-2\text{ = 0} \end{gathered}`

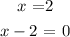
The vertical asymptote is the point where the graph of the function becomes unbounded. It is usually the factor in the denominator.

Given that the vertical asymptote is x = 1, the denominator of the rational function would be (x-1)

The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.

From what we have so far, the degrees of the numerator and denominator are the same, hence, the value given is a multiplier for the factor in the numerator i.e

`f(x)=\text{ }(2(x-2))/(x-1)`

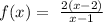
The y-intercept is the point where the curve cuts the y-axis.

From what we have, the y-intercept can be obtained to be 4 by substituting zero for x. The result is 4, which is exactly what we were given.

Hence, the equation given all of the features is:

`f(x)\text{ =}(2(x-2))/(x-1)`