We have the next function

the amplitude is π
The natural frequency is
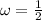
with this, we can calculate the frequency and the period
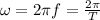
for frequency
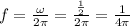
the period is
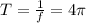
The phase shift is 0
the vertical translation is π
the equation of midline is
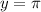
The graph of the function is
where g(x) is the graph in red and the midline is the graph in blue