Question

Diethyl ether is made from ethanol according to thefollowing reaction:2C₂H5OH()Ethanol(C₂H5)₂O(l) + H₂O(l)DiethyletherIn an experiment, 517 g of ethanol gave 391 g ofdiethyl ether. What was the percent yield in thisexperiment?

Answer 1

94.4 %.

Step-by-step explanation:

First, let's see the chemical equation:

`2C_2H_5OH\text{ \lparen ethanol\rparen}\rightarrow(C_2H_5)_2O\text{ \lparen diethyl ether\rparen}+H_2O\text{ \lparen water\rparen}.`

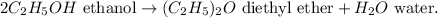
Now, let's calculate the number of moles of ethanol of 517 g of ethanol using its molar mass, which is 46 g/mol, like this:

`517\text{ g ethanol}\cdot\frac{1\text{ mol ethanol}}{46\text{ g ethanol}}=11.2\text{ moles ethanol.}`

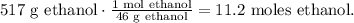
Now, let's see how many moles of diethyl ether can be produced by 11.2 moles of ethanol. You can see in the chemical equation that 2 moles of ethanol reacted produces 1 mol of diethyl ether:

`11.2\text{ moles ethanol}\cdot\frac{1\text{ mol diethyl ether}}{2\text{ moles ethanol}}=5.6\text{ moles diethyl ether.}`

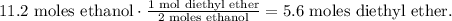
Now, let's convert 5.6 moles of diethyl ether to grams using the molar mass of diethyl ether which is 74 g/mol:

`5.6\text{ moles diethyl ether}\cdot\frac{74\text{ g diethyl ether}}{1\text{ mol diethyl ether}}=414.4\text{ g diethyl ether.}`

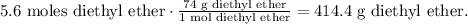
414 g of diethyl ether would be the theoretical yield.

The final step is to calculate the percent yield using the following formula:

`percent\text{ yield=}\frac{actual\text{ yield}}{theoretical\text{ yield}}\cdot100\%.`

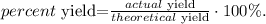
The actual yield of diethyl ether is the given value of the experiment, which is 391 g. If we replace the data that we have, we obtain:

`\begin{gathered} percent\text{ yield=}\frac{391\text{ g}}{414\text{ g}}\cdot100\%, \\ percent\text{ yield=94.4}\%. \end{gathered}`

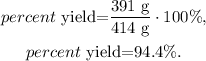
The percent yield of this experiment is 94.4 %.