Question

Line f is graphed on the coordinate grid shown.               What is the slope of a line perpendicular to Line f?

Answer 1

From the property of lines :

If two lines are perpendicular then, the product of the slope of both the lines are equal to ( - 1)

where slope of line is express as :

`\text{ Slope=}(y_2-y_1)/(x_2-x_1)`

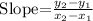
For the slope of the given line,

consider any two coordinates : (-2, 0) & (0,4)

Substitute the coordinates in the expression of the slope,

`\begin{gathered} \text{ Slope=}(y_2-y_1)/(x_2-x_1) \\ \text{Slope}=(4-0)/(0-(-2)) \\ \text{Slope}=(4)/(2) \\ \text{Slope}=2 \end{gathered}`

Slope = 2

Let the slope of the given line is express as m i.e. m = 2

Consider the slope of the line which is perpendicular to given line f is n

Apply the property of line :

Product of slope = (- 1 )

m x n = ( - 1)

Substitute the values :

2 x n = ( -1)

n = (- 1) /2

Slope of the line which is perpendicular to the line f is (-1/2)

Answer : Slope of the line which is perpendicular to the line f is (-1/2)