1 Answer

Ask a Question

Leo Yu · Answer 1 · 2023-11-08T16:41:48+0000

Set a(x)=(1/2)^x; then,

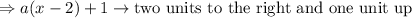
$\Rightarrow a(x-2)+1\to\text{two units to the right and one unit up}$

Furthermore,

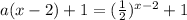
Then, the parent function of function 1) is (1/2)^x.

On the other hand, if b(x)=3^x; then,

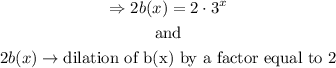
$\begin{gathered} \Rightarrow2b(x)=2\cdot3^x \\ \text{and} \\ 2b(x)\to\text{dilation of b(x) by a factor equal to 2} \end{gathered}$

Therefore, the parent function of 2*3^x is 3^x.

Now, we need to find 9 points on each parent function, as shown below

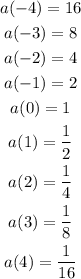
$\begin{gathered} a(-4)=16 \\ a(-3)=8 \\ a(-2)=4 \\ a(-1)=2 \\ a(0)=1 \\ a(1)=(1)/(2) \\ a(2)=(1)/(4) \\ a(3)=(1)/(8) \\ a(4)=(1)/(16) \end{gathered}$

And

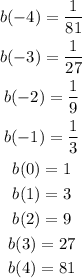
$\begin{gathered} b(-4)=(1)/(81) \\ b(-3)=(1)/(27) \\ b(-2)=(1)/(9) \\ b(-1)=(1)/(3) \\ b(0)=1 \\ b(1)=3 \\ b(2)=9 \\ b(3)=27 \\ b(4)=81 \end{gathered}$

After graphing the points, we get

Parent function of function 1)

Parent function of function 2)

Now, translating the parent function in green two units to the right and 1 unit up, we obtain

In both images, the green curve is 1/2^(x)->parent function of (1/2)^(x-2)+1

the yellow curve is (1/2)^(x-2)+1

The red curve is 3^x->parent function of 2*3^x

and the blue curve is 2*3^x