Question

3. Find all solutions to the equation 3cos(3x) = −7/5 without a calculator

Answer 1

x = 1/3 (arccos (-7/15) + 2πn)

Step-by-step explanation:

For solving for x in

`3\cos \mleft(3x\mright)=-(7)/(5)`

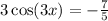
we first divide both sides by 3 to get

`\cos (3x)=-(7)/(3*5)`
`\cos (3x)=-(7)/(15)`

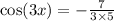
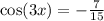
taking the arccos of both sides gives

`\arccos \lbrack\cos 3x\rbrack=\arccos (-(7)/(15))`
`3x=\arccos (-(7)/(15))+2\pi n`

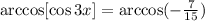
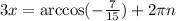
finally, dividing both sides by 3 gives

`\boxed{x=(1)/(3)\lbrack\arccos (-(7)/(15))+2\pi n\rbrack}`

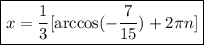
where n is an integer.

We can find the numerical answer for x by using a calculator to find the value of arccos(-7/15).