Question

Emma rode 8 times as fast as Emily . In fact , she rode 48 kilometers in 4 hours less than it took Emily to ride 36 miles . How fast did each of them ride ? How long did they ride ?

Answer 1

Let M be Emma's speed and E be Emily's speed. Since Emma rode 8 times as fast as Emily, we can write it as

`M=8* E`

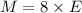
Now, we know that she rode 48 km in 4 hours less than it took Emily to ride 36 miles. This means that

`\begin{gathered} \\ \\ 48km=M*(t-4hours) \end{gathered}`

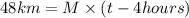
and

`36\text{miles}=E*(t)`

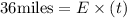
where t denotes the time in which they rode the same distance.

From the second equation,we have

`\begin{gathered} \\ (t-4)=(48)/(M)\ldots(A) \end{gathered}`

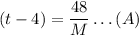
and for the third equation, we have

`\begin{gathered} \\ t=(36)/(E)= \end{gathered}`

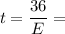
Now, we need to convert units, from miles to kilometers. We know that 1miles is equal to 1.6km, then we get

then, our last equation is equivalent to

`t=(57.6)/(E)\ldots(B)`

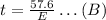
By substituting equation B into equation A, we have

`(57.6)/(E)-4=(48)/(M)\ldots(C)`

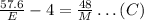
Then, we have 2 equations in 2 unknows, that is, our first equation and equation C. Then, By substituting our first equation into equation C, we have

`\begin{gathered} (57.6)/(E)-4=(48)/(8\cdot E) \\ or \\ (57.6)/(E)-4=(6)/(E) \end{gathered}`

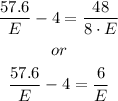
By moving the right hand side to the left hand side and -4 to the right hand side, we have

`(1)/(E)(57.6-6)=4`

which gives

with this result, we can find M by substituting this values into our first equation, that is,

Then, for the first question How fast did each of them ride ? The answer is

Now, in order to find how long they ride, we need to find the time t. We can find it by substituting E into equation B, that is

`\begin{gathered} t=(57.6)/(E) \\ t=(57.6)/(12.9) \\ t=4.46\text{ hour} \end{gathered}`

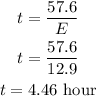
Then, the distance is

`103.2(\frac{km}{\text{hour}})(4.46\text{hour)}=460.8\text{ km}`

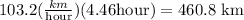
then, How long did they ride ? 460.8 kilometers