Let M be Emma's speed and E be Emily's speed. Since Emma rode 8 times as fast as Emily, we can write it as
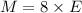
Now, we know that she rode 48 km in 4 hours less than it took Emily to ride 36 miles. This means that
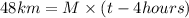
and
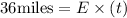
where t denotes the time in which they rode the same distance.
From the second equation,we have
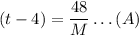
and for the third equation, we have
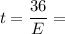
Now, we need to convert units, from miles to kilometers. We know that 1miles is equal to 1.6km, then we get
![\begin{gathered} \\ 36\text{miles}=36\text{miles(}\frac{1.6\operatorname{km}}{1mile})=57.6\text{ km} \end{gathered}]()
then, our last equation is equivalent to
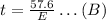
By substituting equation B into equation A, we have
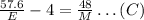
Then, we have 2 equations in 2 unknows, that is, our first equation and equation C. Then, By substituting our first equation into equation C, we have
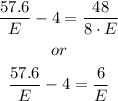
By moving the right hand side to the left hand side and -4 to the right hand side, we have
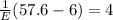
which gives
![\begin{gathered} \\ (51.6)/(E)=4 \\ E=(51.6)/(4) \\ E=12.9(\frac{\operatorname{km}}{hour}) \end{gathered}]()
with this result, we can find M by substituting this values into our first equation, that is,
![\begin{gathered} M=8* E \\ M=8*12.9 \\ M=103.2(\frac{\operatorname{km}}{hour}) \end{gathered}]()
Then, for the first question How fast did each of them ride ? The answer is
![\begin{gathered} \text{Emma's sp}eed=103.2\text{ }\frac{\operatorname{km}}{hour} \\ \text{Emily's sp}eed=12.9\text{ }\frac{\operatorname{km}}{hour} \\ \end{gathered}]()
Now, in order to find how long they ride, we need to find the time t. We can find it by substituting E into equation B, that is
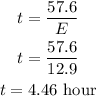
Then, the distance is
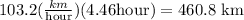
then, How long did they ride ? 460.8 kilometers