Question

A manufacturer knows that their items have a normally distributed length, with a mean of 10.8 inches, and standard deviation of 0.9 inches.If one item is chosen at random, what is the probability that it is less than 8.4 inches long?

Answer 1

We need to find the probability:

`P(X<8.4)`

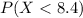
where X is a normal random variable with mean 10.8 and standard deviation 0.9. To find this probability we need to use the z-score formula so we can use the standard normal distribution. The z-score is given by:

`z=(x-\mu)/(\sigma)`

where μ is the mean and σ is the standard deviation. In this case the z-score is given as:

`\begin{gathered} z=(8.4-10.8)/(0.9) \\ z=-2.67 \end{gathered}`

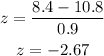
Then we have that:

`P(X<8.4)=P(z<-2.67)`

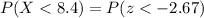
Looking for the probability on the right side of the previous expression in the standard table we have that:

`P(X\lt8.4)=P(z\lt-2.67)=0.0038`

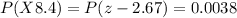
Therefore, the probability of choosing an item with length less than 8.4 inches is 0.0038