We need to find the probability:
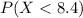
where X is a normal random variable with mean 10.8 and standard deviation 0.9. To find this probability we need to use the z-score formula so we can use the standard normal distribution. The z-score is given by:
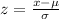
where μ is the mean and σ is the standard deviation. In this case the z-score is given as:
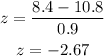
Then we have that:
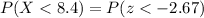
Looking for the probability on the right side of the previous expression in the standard table we have that:
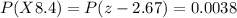
Therefore, the probability of choosing an item with length less than 8.4 inches is 0.0038