Question

A ball is thrown into the air by a baby alien on a planet in che system of Alpha Centauri with a velocity of 34 ft/s, Its height in feet after t seconds is given by y = 34t - 14t^2 A. Find the average velocity (include units help (units)) for the time period beginning when t = 2 and lasting.01 s:.005 s:.002 s:.001 s:B. Estimate the instantaneous velocity when t= 2 include unitsAnswer:

Answer 1

We are given that the function of velocity for a given object is the following:

`y=34t-14t^2`

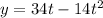
To determine the average velocity we will use the following formula:

`v=(y_f-y_0)/(t_f-t_0)`

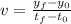
Where:

`\begin{gathered} y_f,y_0=\text{ final and initial positions} \\ t_f,t_0=\text{ final and initial time} \end{gathered}`

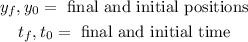
To determine the initial position we will substitute the value "t = 2" in the function for the position:

`y(2)=34(2)-14(2)^2`

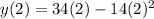
Solving the operations:

`y(2)=12`

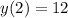
Now, to determine the final position we will use the second time point. In this case, we are given that for the final position the time has lasted 0.01s, this means that the value of "t" is:

`t_f=2+0.01=2.01`

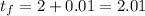
Now, we substitute in the function for the velocity:

`y(2.01)=34(2.01)-14(2.01)^2`

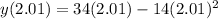
Solving the operations:

`y(2.01)=11.78`

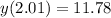
Now, we substitute in the formula for the average velocity:

`v=(11.78-12)/(0.01)`

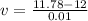
Solving the operations:

`v=-22(ft)/(s)`

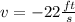
Therefore, the average velocity after 0.01s is -22 ft/s.

The same procedure can be used to determine the average velocity for the different times.

Part B. To determine the instantaneous velocity we will use the fact that the velocity is the derivative of the position with respect to time:

`v=(dy)/(dt)`

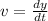
Now, we determine the derivative of the function:

`(dy)/(dt)=(d)/(dt)(34t-14t^2)`

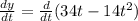
Now, we distribute the derivative:

`(dy)/(dt)=(d)/(dt)(34t)-(d)/(dt)(14t^2)`

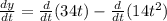
Now, we determine the derivative using the following rule:

`(d)/(dx)(ax^n)=\text{nax}^(n-1)`

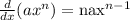
Applying the property we get:

`(dy)/(dt)=34-28t`

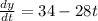
Now, we substitute the value "t = 2" to get the velocity:

`(dy)/(dt)=34-28(2)`

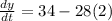
Solving the operations:

`(dy)/(dt)=-22`

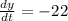
Therefore, the instantaneous velocity at "t = 2" is -22 ft/s