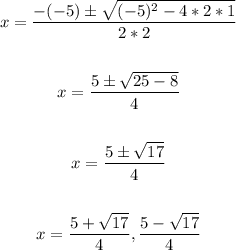Question

Select that two values of x that are roots of thi equation

Answer 1

B.

`x=(5+√(17))/(4)`

C.

`x=(5-√(17))/(4)`

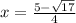
Step-by-step explanation:

Given:

`2x^2+1=5x`

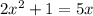
To find:

The two values of x that are roots of the equation

Let's subtract 5x from both sides of the equation;

`\begin{gathered} 2x^2+1-5x=5x-5x \\ 2x^2-5x+1=0 \end{gathered}`

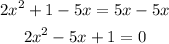
Recall that a quadratic equation is generally given in the below form;

`ax^2+bx+c=0`

Comparing both equations, we can see that;

`\begin{gathered} a=2 \\ b=-5 \\ c=1 \end{gathered}`

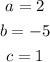
Let's go ahead and use the below quadratic formula to solve for the values of x;

`x=(-b\pm√(b^2-4ac))/(2a)`
`\begin{gathered} x=(-(-5)\pm√((-5)^2-4*2*1))/(2*2) \\ \\ x=(5\pm√(25-8))/(4) \\ \\ x=(5\pm√(17))/(4) \\ \\ x=(5+√(17))/(4),(5-√(17))/(4) \end{gathered}`