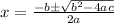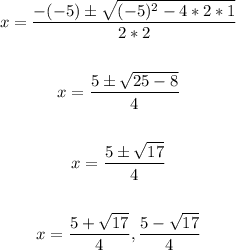ANSWER:
B.
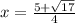
C.
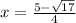
Step-by-step explanation:
Given:
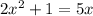
To find:
The two values of x that are roots of the equation
Let's subtract 5x from both sides of the equation;
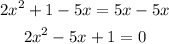
Recall that a quadratic equation is generally given in the below form;

Comparing both equations, we can see that;
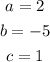
Let's go ahead and use the below quadratic formula to solve for the values of x;