Question

For each system of equations below, determine whether it has one solution, no solutions, or infinite solutions.x-3y=8-2x+6y=8

Answer 1

To determine if the system has one solution, first write one of the equations for one of the variables:

`\begin{gathered} 1)\text{ x-3y=8} \\ 2)\text{ -2x+6y=8} \end{gathered}`

I'll write the first equation for x:

`\begin{gathered} x-3y=8 \\ x=8+3y \end{gathered}`

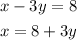
Next replace it in the second equation

`-2(8+3y)+6y=8`

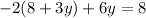
And solve for y.

Using the distributive property of multipication solve the term in parentheses:

`\begin{gathered} (-2)\cdot8+(-2)(3y)+6y=8 \\ -16-6y+6y=8 \\ -16=8 \end{gathered}`

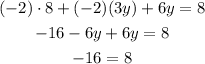
The result for this equatio nsystem is -16=8 → this is a false statement, which means that the system has no solution, if you were to grapf the equations, the li