To determine if the system has one solution, first write one of the equations for one of the variables:
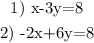
I'll write the first equation for x:
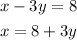
Next replace it in the second equation
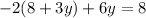
And solve for y.
Using the distributive property of multipication solve the term in parentheses:
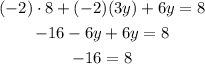
The result for this equatio nsystem is -16=8 → this is a false statement, which means that the system has no solution, if you were to grapf the equations, the li