Given:
The mass of the car is,
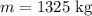
The radius of the circular path is,
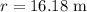
The coefficient of friction between the tires and the road is,
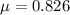
The acceleration due to gravity is,
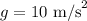
To find:
How fast (in m/s) can the car go without skidding off the turn
Step-by-step explanation:
The frictional force balances the centripetal force.
The frictional force is,
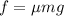
The centripetal force is,
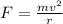
Here, v is the speed of the car without skidding.
We can write,
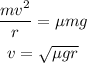
Substituting the values we get,
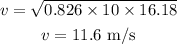
Hence, the required speed is 11.6 m/s.