Solution:
The circumradius of the polygon is given below as

Concept:
The perimeter of the nonagon will be calculated using the formula below
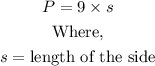
The Length of a side can be calculated using the formula below
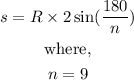
By substituting the values, we will have
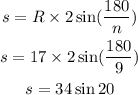
Hence,
Substitute the value of s=34sin20 to get the perimeter in the formula below
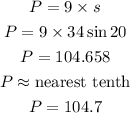
Hence,
The final answer is P =104.7 units