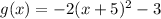Question

I am confused on this problem and am looking for help. If anyone could help me it would be appreciated

Answer 1

`g(x)=-2(x+5)^(2)-3`

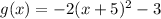
0. Horizontal translation 5 units.

,

1. Reflection over the x-axis

,

2. Vertical compression 2 units

,

3. Vertical translation down 3 units

`y=-(x+5)^2`

Step-by-step explanation

• Writing the function in completed-square form.

As a ≠ 1, where a is the coefficient of the leading term, to write it in the completed-square form we have to make a = 1:

`g(x)=-2x^2-20x-53`
`g(x)=-2(x^2+10x+(53)/(2))`

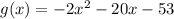
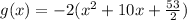
Now we have to take half of the x term and square it and add it to the function as follows:

`(10)/(2)^2=5^2=25`
`g(x)=-2((x^2+10x+25)+(53)/(2)-25)`

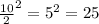
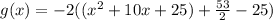
Finally, we have a Perfect Squared Trinomial in the left side that we can rewrite as follows, obtaining our function g(x):

`g(x)=-2(x+5)^2+(3\cdot-2)/(2)`
`g(x)=-2(x+5)^2-3`

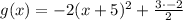
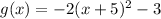
As our parent function is:

`f(x)=x^2`

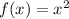
Then, the transformations that suffered were:

• Horizontal translation to the left 5 units

`y=(x+5)^2`

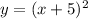
• Reflection over the x-axis

`y=-(x+5)^2`

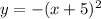
• Vertical compression 2 units

`y=-2(x+5)^2`

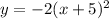
• Vertical translation down 3 units

`g(x)=-2(x+5)^(2)-3`