Since the number of bacteria in a colony doubles every 237 hours, this growth has an exponential behavior. Every cicle of 237 hours, the population multiplies by 2. The following function models this behavior
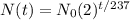
N_0 represents the initial value of the population and t represents the time in hours. There is currently a population of 479,000 bacteria, which means that our function is
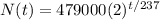
To find the population after 948, we just need to evaluate t = 948 in our function.

After 948, the population will be 7,664,000 bacteria.