Answer: 10.3
Given:
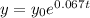
We are to find how many hours would it take for the size of the samples to double. Given that y is the number present at t hours, we know that we need to find how long would it take for y = 2y0.
We can now solve this by substituting y = 2y0
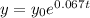
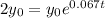
*cancel out y0
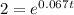
*solve for t
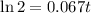

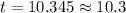
Therefore, at 10.3 hours, the sample will double in size.