Question

36. If the interest rate on a 30-year mortgage for $325,000 were changed from 2.9% to 2.6%, how much would you save over the life of the loan?

Answer 1

The formula to calculate the mortgage payment is as follows:

`M=P(\lbrack i(1+i)^n\rbrack)/(\lbrack(1+i)^n-1\rbrack)`

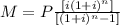
Where P is the principal loan amount $325,000

i is the monthly interest rate, divide the annual interest rate by 12 to find the monthly interest rate.

n is the number of payments over the lifetime of the loan (months) then as you have a 30-year mortgage n=30 years x 12 months per year=360 payment months.

a. For 2.9% interest rate:

i=2.9%/12=0.029/12=0.002417

Replace the known values:

`\begin{gathered} M1=325,000(\lbrack0.002417(1+0.002417)^(360)\rbrack)/(\lbrack(1+0.002417)^(360)-1\rbrack) \\ M1=325,000(\lbrack0.002417\cdot2.38441\rbrack)/(\lbrack2.38441-1\rbrack) \\ M1=325,000(0.005762)/(1.38441) \\ M1=1352.75 \end{gathered}`

This would be the monthly payment when interest rate is 2.9%

b. For 2.6% interest rate:

i=2.6%/12=0.026/12=0.002167.

`\begin{gathered} M2=325,000(\lbrack0.002167(1+0.002167)^(360)\rbrack)/(\lbrack(1+0.002167)^(360)-1\rbrack) \\ M2=325,000(\lbrack0.002167\cdot2.17963\rbrack)/(\lbrack2.17963-1\rbrack) \\ M2=325,000(0.004723)/(1.17963) \\ M2=1301.1 \end{gathered}`

Thus, to calculate how much would you save over the life of the loan, multiply each monthly payment by 360 payments, and the difference would be the money you save:

`\begin{gathered} At\text{ 2.9\% interest rate:} \\ 1352.75*360=486989.1 \\ At\text{ 2.6\% interest rate:} \\ 1301.1*360=468397.5 \\ \text{Money saved: }486989.1-468397.5=18591.6 \end{gathered}`

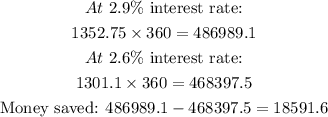
Answer: You save $18591.6 over the life of the loan if the interest changed from 2.9% to 2.6%