The formula to calculate the mortgage payment is as follows:
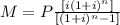
Where P is the principal loan amount $325,000
i is the monthly interest rate, divide the annual interest rate by 12 to find the monthly interest rate.
n is the number of payments over the lifetime of the loan (months) then as you have a 30-year mortgage n=30 years x 12 months per year=360 payment months.
a. For 2.9% interest rate:
i=2.9%/12=0.029/12=0.002417
Replace the known values:

This would be the monthly payment when interest rate is 2.9%
b. For 2.6% interest rate:
i=2.6%/12=0.026/12=0.002167.

Thus, to calculate how much would you save over the life of the loan, multiply each monthly payment by 360 payments, and the difference would be the money you save:
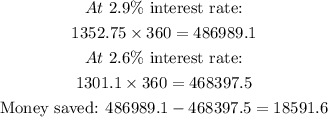
Answer: You save $18591.6 over the life of the loan if the interest changed from 2.9% to 2.6%