Question

Given that R is between A and X on a segment, draw a picture and write an equationusing the Segment Addition Postulate. Then find AR and RX if AR = 5x - 15,RX = 3x + 1, and AX = 58.

Answer 1

The segment addition postulate states that if we are given two points on a line segment, A and C, a third point B lies on the line segment AC

if and only if the distances between the points meet the requirements of the equation AB + BC = AC.

The picture can look roughly like this:

We can see that "R" is in-between "A" and "X".

From the postulate, we can write:

AR + RX = AX

Now,

Given

AR = 5x - 15

RX = 3x + 1

AX = 58,

We put it into the equation and find x first. Shown below:

`\begin{gathered} AR+RX=AX \\ (5x-15)+(3x+1)=58 \\ 5x+3x-15+1=58 \\ 8x-14=58 \\ 8x=58+14 \\ 8x=72 \\ x=(72)/(8) \\ x=9 \end{gathered}`

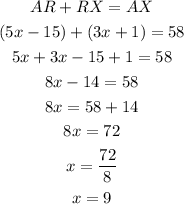
Since, we got x, we can easily find AR and RX. Shown below:

AR = 5x - 15

AR = 5(9) - 15

AR = 45 - 15

AR = 30

and

RX = 3x + 1

RX = 3(9) + 1

RX = 27 + 1

RX = 28