Given the figure shown in the exercise, you can identify that it is formed by a triangle and a rectangle. Then, the total area of the figure will be the sum of the area of the triangle and the area of the rectangle.
• The formula for calculating the area of a rectangle is:
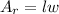
Where "l" is the length and "w" is the width.
In this case:
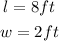
Then, by substituting the values into the formula and evaluating, you get:
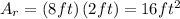
• The formula for calculating the area of a triangle is:
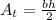
Where "b" is the base and "h" is the height of the triangle.
In this case, you can identify that:

See the picture below:
Knowing the base and the height of the triangle, you can substitute values into the formula and evaluate, in order to find its area:
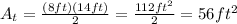
Therefore, you can determine that the total area of the figure is:

Hence, the answer is:
