ANSWER:
DE = 2.5 units
EDF = 74°
Explanation:
The first thing in this case is to calculate the ratio between both triangles with the known sides BC and EF:
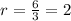
Now, this ratio is conserved in all the triangles since they are similar, therefore, we calculate the DE value like this:
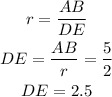
Being similar triangles, the angles are equal, we know that an isoceles triangle, because it has two equal sides, therefore, it also has two equal angles and knowing that the sum of the internal angles in a triangle is equal to 180 degrees, we can calculate the value of the angle EDF, just like this:
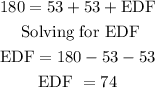
If length of EF is 3 units, then the length of DE is 2.5 units. If m