Question

Graph the system of inequalities and shade in the solution set. If there are no solutions,graph the corresponding lines and do not shade in any region Y is greater and equal to 2/3 - 1 Y < -x + 3

Answer 1

The given system of inequalities is:

`\begin{gathered} y\ge(2)/(3)-1 \\ y<-x+3 \end{gathered}`

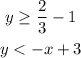
The first inequality is a horizontal line at:

`\begin{gathered} y\ge(2\cdot1-3\cdot1)/(3) \\ y\ge(2-3)/(3) \\ y\ge(-1)/(3) \end{gathered}`

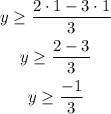
The solution to this inequality is all the y-values greater or equal to -1/3:

Now, for the second inequality, let's make a table of values to draw the line and the solution set.

When x=0:

`\begin{gathered} y=-0+3 \\ y=3 \end{gathered}`

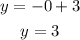
The first point on the line is (0,3).

When x=1, then:

`\begin{gathered} y=-1+3 \\ y=2 \end{gathered}`

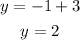
The second point on the line is (1,2).

And when x=-1:

`\begin{gathered} y=-(-1)+3 \\ y=1+3 \\ y=4 \end{gathered}`

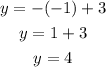
The third point on the line is (-1,4).

With these three points, we can draw the base-line for the inequality, but as it is y<-x + 3, the solution set is the values lower than the line, without including the line itself, then it is:

If we overlap both inequalities, we obtain:

The solution set is the region that can be seen in purple, where both graphs overlap.