The given system of inequalities is:
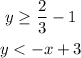
The first inequality is a horizontal line at:
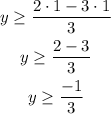
The solution to this inequality is all the y-values greater or equal to -1/3:
Now, for the second inequality, let's make a table of values to draw the line and the solution set.
When x=0:
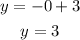
The first point on the line is (0,3).
When x=1, then:

The second point on the line is (1,2).
And when x=-1:
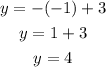
The third point on the line is (-1,4).
With these three points, we can draw the base-line for the inequality, but as it is y<-x + 3, the solution set is the values lower than the line, without including the line itself, then it is:
If we overlap both inequalities, we obtain:
The solution set is the region that can be seen in purple, where both graphs overlap.