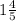We need to find the value of the expression:
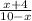
when x = 5.
In order to do so, we can replace x with 5 in the expression above. We obtain:

This is the value written as a fraction. We can divide 9 by 5 to obtain the number:
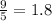
We can also write it as a mixed number:
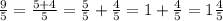
Answer: