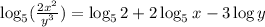Question

Please help me on 1I’m confused Please show work so I can understand

Answer 1

`\log _52+2\log _5x^{}-3\log y`

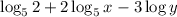
Explanation:

Given the logarithm expression:

`\log _5\mleft((2 x^(2))/(y^(3))\mright)`

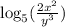
To expand the expression, follow the steps below:

Step 1: Apply the division law of logarithm below. That is, the log of a quotient is the difference between the logs. Therefore:

`\begin{gathered} \log ((A)/(B))=\log (A)-\log (B) \\ \implies\log _5\mleft((2 x^(2))/(y^(3))\mright)=\log _5(2x^2)-\log (y^3) \end{gathered}`

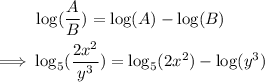
Step 2: Similarly, by the multiplication law, the log of a product is the sum of the logs.

`\begin{gathered} \log (AB)=\log (A)+\log (B) \\ \log _5(2x^2)=\log _52+\log _5x^2 \\ \implies\log _5(2x^2)-\log (y^3)=\log _52+\log _5x^2-\log (y^3) \end{gathered}`

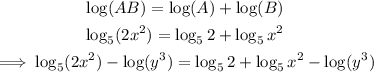
Step 3: We apply the index law of logarithm.

If the number whose logarithm we are looking for has an index (or power), we can write the index as a product.

`\log x^n=n\log x`

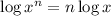
So, we have that:

`\implies\log _5(2x^2)-\log (y^3)=\log _52+2\log _5x^{}-3\log y`

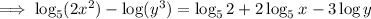
Thus, the expanded form of the given expression is:

`\log _5\mleft((2 x^(2))/(y^(3))\mright)=\log _52+2\log _5x^{}-3\log y`