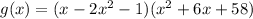Question

For the polynomial below, 1 is a zero of multiplicity twog(x) = x^4+ 4x^3 +47x^2 - 110x+ 58 Express g (x) as a product of factors. g(x) = ?

Answer 1

Given:

The given polynomial is

`g(x)=x^4+4x^3+47x^2-110x+58`

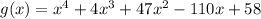
1 is a zero of multiplicity two.

Required:

We have to express g(x) as a product of linear factors.

Step-by-step explanation:

Since 1 is a zero of multiplicity two,

`(x-1)^2`

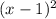
is a factor of g(x).

So we can divide g(x) by

`(x-1)^2=x^2-2x+1.`
`g(x)=\text{ \_\_\_}(x^2-2x+1)+\text{ \_\_\_}(x^2-2x+1)+\text{ \_\_\_\_}`

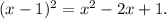
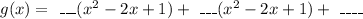
We will fill the blanks with suitable terms.

`\begin{gathered} g(x)=x^2(x-2x^2-1)+6x(x-2x^2-1)+58(x-2x^2-1) \\ g(x)=(x-2x^2-1)(x^2+6x+58) \end{gathered}`

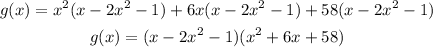
Final answer:

Hence the final answer is

`g(x)=(x-2x^(2)-1)(x^(2)+6x+58)`