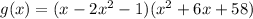Given:
The given polynomial is
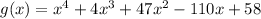
1 is a zero of multiplicity two.
Required:
We have to express g(x) as a product of linear factors.
Step-by-step explanation:
Since 1 is a zero of multiplicity two,
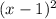
is a factor of g(x).
So we can divide g(x) by
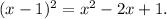
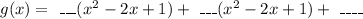
We will fill the blanks with suitable terms.
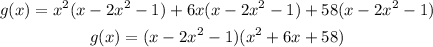
Final answer:
Hence the final answer is