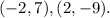Question

A line passes through the point (-1,3) and (1,-5). Which points lie on the same line?

Answer 1

To determine which points are on the line, first, we compute the equation of the line. To determine the equation of a line that passes through two points we can use the following formula:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1).`

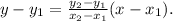
Using the above formula, we get that the equation of a line that passes through the given points is:

`\begin{gathered} y-3=(-5-3)/(1-(-1))(x-(-1)), \\ y-3=(-8)/(2)(x+1). \\ y-3=-4x-4, \\ y=-4x-1. \end{gathered}`

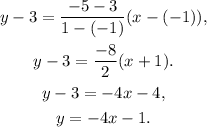
Now, we evaluate the above equation at every x-entry of the points in the options, if the result of the evaluation is the corresponding y-entry, then the point is on the line:

`\begin{gathered} x=-2;\text{ }y=-4(-2)-1=8-1=7, \\ x=-5;\text{ }y=-4(-5)-1=20-1=19, \\ x=4;\text{ }y=-4(4)-1=-16-1=-17, \\ x=2;\text{ }y=-4(2)-1=-8-1=-9, \\ x=-3;\text{ }y=-4(-3)-1=12-1=11, \\ x=0;\text{ }y=-4(0)-1=0-1=-1. \end{gathered}`

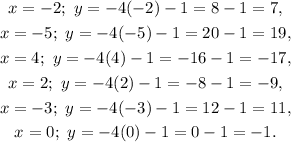
There the following points are on the line:

`(-2,7),(-5,19),(4,-17),(2,-9),(-3,11),(0,-1).`

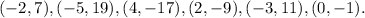
Answer:

`(-2,7),(2,-9).`