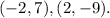To determine which points are on the line, first, we compute the equation of the line. To determine the equation of a line that passes through two points we can use the following formula:
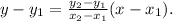
Using the above formula, we get that the equation of a line that passes through the given points is:
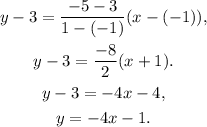
Now, we evaluate the above equation at every x-entry of the points in the options, if the result of the evaluation is the corresponding y-entry, then the point is on the line:
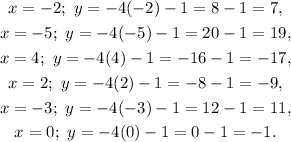
There the following points are on the line:
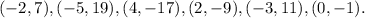
Answer: