Question

A piece of sheet metal, w = 20 inches wide, is bent to form the guttershown in the illustration. If the cross-sectional area is 18 square inches,find the depth of the gutter.Tho Yilar County News earns a profit of $20 per year for each of its 3,000

Answer 1

The depth of the gutter can either be 1 inch or 9 inches.

Since the gutter is shaped like a rectangle; Then we can use the formula for the cross-sectional area of a rectangle:

• A = base × height
• base = w - 2x ; w = 20
• height = x
• Area = 18 in²

Now we have :

18 = (w - 2x)(x)

18 = wx - 2x²

Input w = 20

18 = 20x - 2x²

2x² - 20x + 18 = 0

x² - 10x + 9 = 0

x(x - 1) -9(x - 1) = 0

x = 1 or x = 9

x = height = depth

X = 9 inches or x = 1 inch

Hence, the depth of the gutter can either be 1 inch or 9 inches.

Answer 2

The width of the sheet is 20 inches:

`w=20`

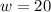
The cross-sectional area is 18 square inches.

From the diagram provided, the cross-sectional area is calculated to be:

`A=(w-2x)(x)`

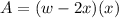
Therefore, we have that:

`(w-2x)(x)=18`

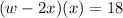
Expanding the equation, we have:

`wx-2x^2=18`

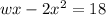
If we substitute the value of w into the equation, we have:

`20x-2x^2=18`

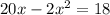
We can divide through by 2 and rearrange the equation. Thus, we have:

`x^2-10x+9=0`

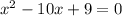
Solving the quadratic equation by factorization, we have:

`\begin{gathered} x^2-9x-x+9=0 \\ x(x-9)-1(x-9)=0 \\ (x-9)(x-1)=0 \\ \therefore \\ x=9\text{ or 1} \end{gathered}`

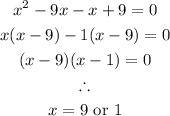
Therefore, the depth of the gutter can be 1 inch or 9 inches.