Question

An object of charge +2.0 x10^-3 C is located at the Cartesian origin, (0m,0m). A second object, of charge -4.0x10^-3 C, is located at a position (50m, 0m). Find the full magnitude and direction of the Electric force present on a test charge of +1C, located at a position (0m, 50m).

Answer 1

Step-by-step explanation:

We can represent the situation with the following figure

Therefore, we need to calculate the magnitude of F1 and F2.

The magnitude of electric force between two charges is equal to

`F=k(q_1q_2)/(r^2)`

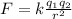
Where k = 8.98 x 10^9, q1 and q2 are the charges and r is the distance between the charges. The distance between the object of charge -4 x 10^(-3) C and the object of charge +1C can be calculated using the Pythagorean theorem as

`\begin{gathered} \text{ Pythagorean Theorem: c=}√(a^2+b^2) \\ \\ \text{ Replacing a = 50 and b = 50} \\ c=√(50^2+50^2) \\ c=√(2500+2500) \\ c=√(5000) \\ c=70.71\text{ m} \end{gathered}`

Therefore, the distance between the charges is 70.71 m.

Then, replacing q1 = -4 x 10^(-3) C, q2 = +1C and r = 70.71 m, on the initial equation, we get:

`\begin{gathered} F1=(8.98*10^9)((-4*10^(-3))(+1))/(70.71^2) \\ \\ F1=7184\text{ N} \end{gathered}`

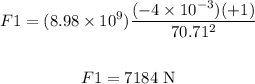
To calculate F2, we need to replace q1 = +2 x 10^(-3) C, q2 = +1C, and r = 50 m, so

`\begin{gathered} F2=(8.98*10^9)((2*10^(-3))(1))/(50^2) \\ \\ F2=7184\text{ N} \end{gathered}`

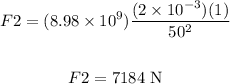
Now, we need to calculate the resultant force, so we need to identify the x and y coordinates of each force and add them

`\begin{gathered} F1x=F1\cos(45)=7184\cos45=5079.86 \\ F1y=F1\sin(45)=7184\sin45=-5079.86 \\ F2x=0 \\ F2y=F2=7184 \\ \\ \text{ Resultant force} \\ Fx=F1x+F2x \\ Fx=5079.86+0=5079.86\text{ N} \\ \\ Fy=F1y+F2y \\ Fy=-5079.86+7184=2104.14\text{ N} \end{gathered}`

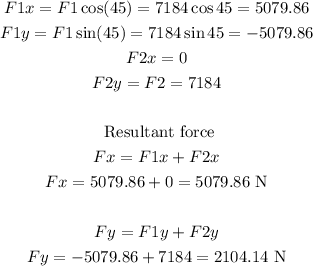
Finally, we can calculate the magnitude and direction of the force as follows

`\begin{gathered} \text{ magnitude } \\ F=√((Fx)^2+(Fy)^2) \\ F=√((5079.86)^2+(2104.14)^2) \\ F=5498.40\text{ N} \\ \\ \text{ Direction} \\ \theta=\tan^(-1)((Fy)/(Fx)) \\ \\ \theta=\tan^(-1)((2104.14)/(5079.86)) \\ \\ \theta=\tan^(-1)(0.41) \\ \theta=22.5° \end{gathered}`

Therefore, the magnitude of the electric force is 5498.40 N and the direction is 22.5 degrees.